

Geodesy
Unlike the standard globe found in many elementary school classrooms,
the earth is not a perfect sphere. The Earth is shaped more like
a beach ball that is being slightly squeezed, a shape that is
known as an ellipsoid. Imagine that the Earth is being squeezed
at the North and South Poles, making it fatter around the equator.
The surface of the Earth is also not perfectly smooth; it is more
like the surface of an orange. From a distance the orange peel
looks smooth, but if you look closer, it is covered in lumps and
dents, similar to how the earth looks smooth in photographs taken
from space, but it is really covered with mountains and valleys.
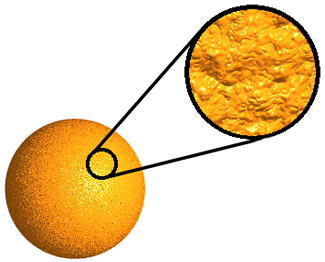
The orange appears smooth, but actually has an irregular surface.
Ellipsoid and Geoid Models
Although the Earth is not perfectly spherical or perfectly smooth,
it can be useful to represent it as a perfect mathematical shape.
There are several ellipsoids models that are used for different
purposes in different parts of the world, due to the fact that
different shapes may be a better fit to the actual shape of the
earth in different places. The U.S. Department of Defense developed
GPS around the World Geodetic System 1984 (WGS84) reference system,
part of which is the WGS84 ellipsoid.
There is also another type of model used to represent the surface
of the Earth, called the geoid model. The NOAA's National Geodetic
Society defines the geoid as “the equipotential surface
of the Earth's gravity field which best fits, in a least squares
sense, global mean sea level.” More simply put, the strength
of Earth's gravitational field is not the same in all locations
on the actual surface of the Earth. When a geoid model is made
the actually shape of the earth is manipulated so that all of
the points on the new, imaginary surface would experience the
same gravitational pull.
WGS84
The WGS84 reference system is used for real-time GPS measurements
and calculations. The resultant coordinates are relater to the
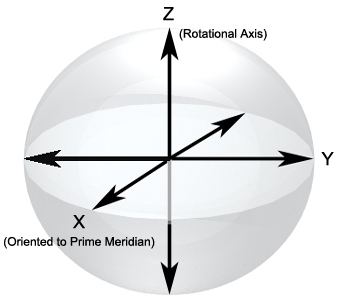
WGS84 ellipsoid model. The origin of WGS84 ellipsoid coincides
with the center of the Earth’s mass. The perpendicular X
and Y axes form the equatorial plane. The Z axis is perpendicular
to this plane, and coincides with the Earth’s rotational
axis. The X axis is oriented to the Prime Meridian.
Top of Page
Global Positioning Systems : Next >>
GPS Positioning
